Uniform Manifold Approximation and Projection- UMAP
or how a Muggle can perform Math Magic....
I recently had to perform a large amount of dimensionality reduction - & as such needed to consider how to do it - in the end I went with UMAP. It is a relatively new technique so I figured that putting down some thoughts may be of interest.
Dimensionality reduction
The first thing that I needed to understand is what problem is dimensionality reduction addressing? I like this definition:
Find a low-dimensional representation of the data that captures as much of the information as possible - Air Force Institute of Technology
So quite a lofty goal, despite sounding attractively simple. I should note that there are other other uses for dimensionality reduction, including addressing the 'curse of dimensionality'. (Which, is perhaps the most Harry Potter-esque term that I've encountered in deep learning yet - us poor Muggles, so many problems visualizing N-D space ...) However, using dimensionality reduction in order to enable visualization is the main use that I want to focus on, primarily because of my final project and challenges therein. In Deep learning and machine learning, with the complexity of the neural networks that are being constructed, it's hard to visualize what is happening in the different layers (as an aside, reminded me of the book Flatland, published in 1884). This is not only due to the dimensionality of layers used, but the complexity of the networks - there's a reason that another name for GoogLeNet is Inception. So for me, the problem that dimensionality reduction is addressing is "making it easier to visualize the data when reduced to very low dimensions such as 2D or 3D", as per Wikipedia.
So what is UMAP?
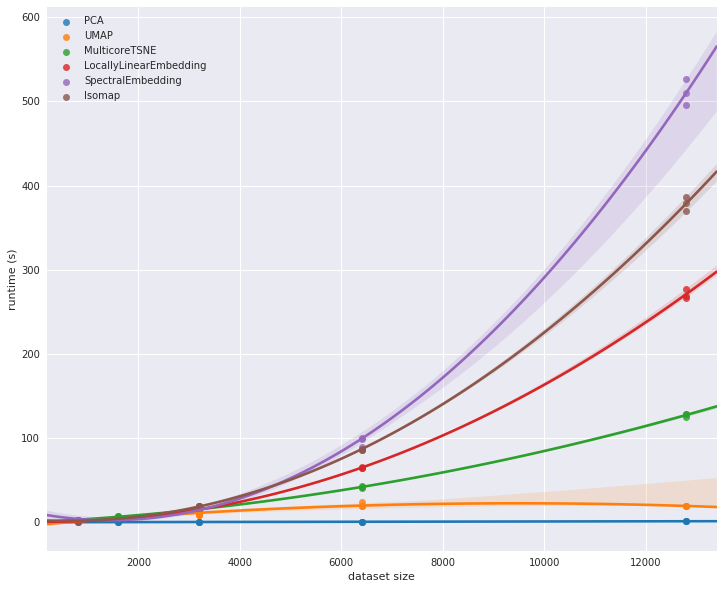
In terms of dimensionality reduction, there are a lot of options, among them PCA, spectral and local linearly embedding, t-SNE, UMAP, etc. All of them have pros & cons - but what I wanted to optimize for in choosing a reduction technique was both robustness of embedding and speed - I think that this graph should show why I considered UMAP the leading contender (PCA, being linear, doesn't extend itself too well to non-linear structures such as images):
Moreover, I should note that UMAP was invented by Leland McInnes, a fellow Antiopedian, so Southern Hemisphere represent... All joking aside, in the words of Leland himself, UMAP:
“is an unsupervised learning technique for dimension reduction/manifold learning. It provides a way to find a simpler representation of your data by reducing the dimensionality. This is similar to the way clustering is an unsupervised learning technique which tries to find a simpler representation of your data by breaking it up into clusters...Finally it can be used for post-processing analysis. Suppose you have trained a convolutional neural net for image classification. You can apply dimension reduction to the next to last layer outputs to provide some understanding of the image space that the network has constructed.”
Thus, it seemed perfect for the task I had at hand - visualizing multiple dimensions in the 2 that my homo sapiens mind can contemplate. Now, we can get into the specifics of UMAP, but this is supposed to be a short blog post. This is Lelands simple version of the mechanics (yes, I said simple):
Assume the data is uniformly distributed on the manifold (the U in the name). That assumption can be used to approximate the volume form and (given suitable approximations from local distributions) thence the metric tensor local to each data point. If we assume that the metric tensor is locally constant we can create (different, incompatible) metric spaces locally for each data point. We can then push this through David Spivak's Metric-Space/Fuzzy-Simplicial-Set adjunction, or, if you prefer, build a fuzzy open cover (fuzzy as we degrade confidence in our local metric space) and construct the fuzzy Cech-complex associated to it. This is the M and A part (manifold approximation via a fuzzy simplicial complex).
And so on and so forth. However, for those of us who aren't constantly improving our Erdős number, I suggest the talk that Leland gave at PyData, and his reddit post on the subject, both of which are targeted towards a larger audience than mathematicians. (He is very responsive on github issues too btw). To give the briefest of biased highlights:
It is compatible with t-SNE as a drop-in replacement, so you can use code with minimal disruption.
It preserves more global structure than other metrics (people far more qualified than I have agreed with this point ..)
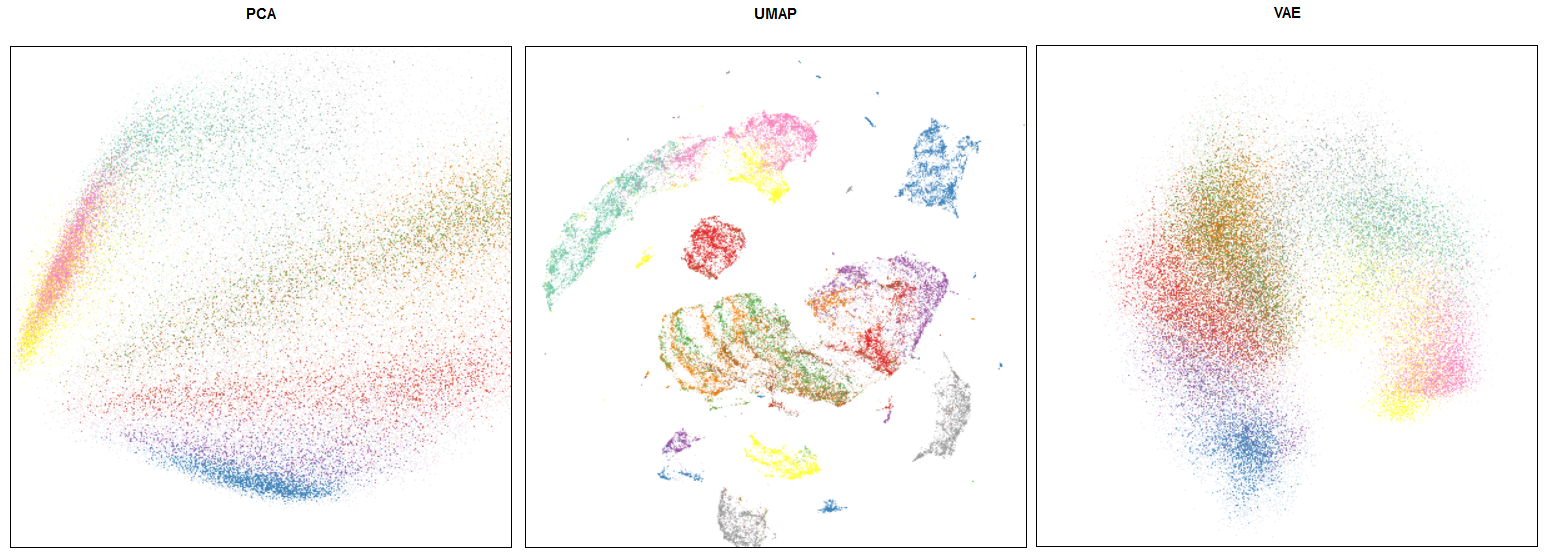
Comparision of UMAP/PCA/VAE embeddings for Fashion MNIST, from https://umap-learn.readthedocs.io/en/latest/faq.html
Did I mention faster?
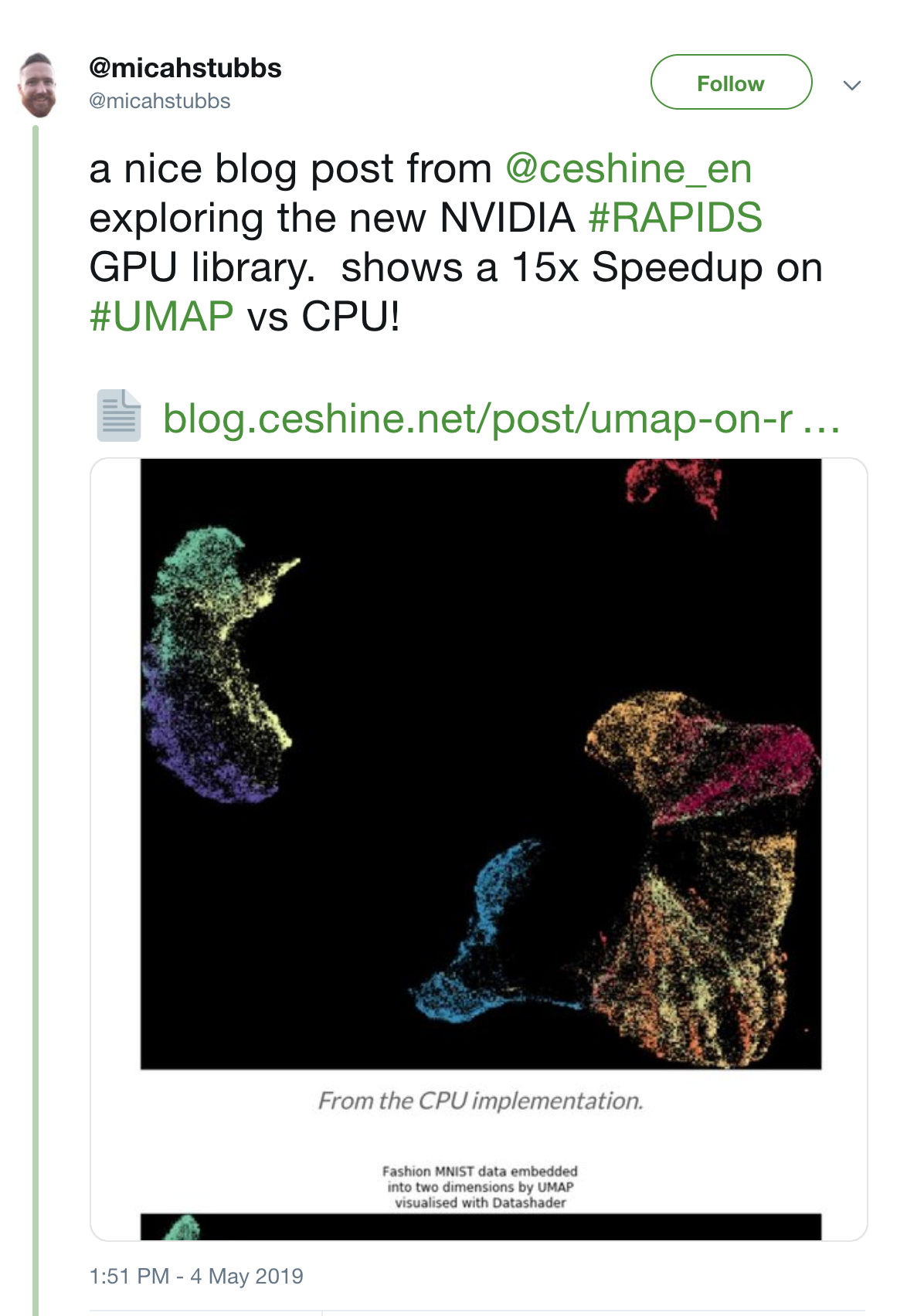
In addition, UMAP implementation has the potential to be even faster, as it uses optimization performed via a custom stochastic gradient descent. The RAPIDS team from NVIDIA has published a GPU implementation, and stated a 15x speedup:
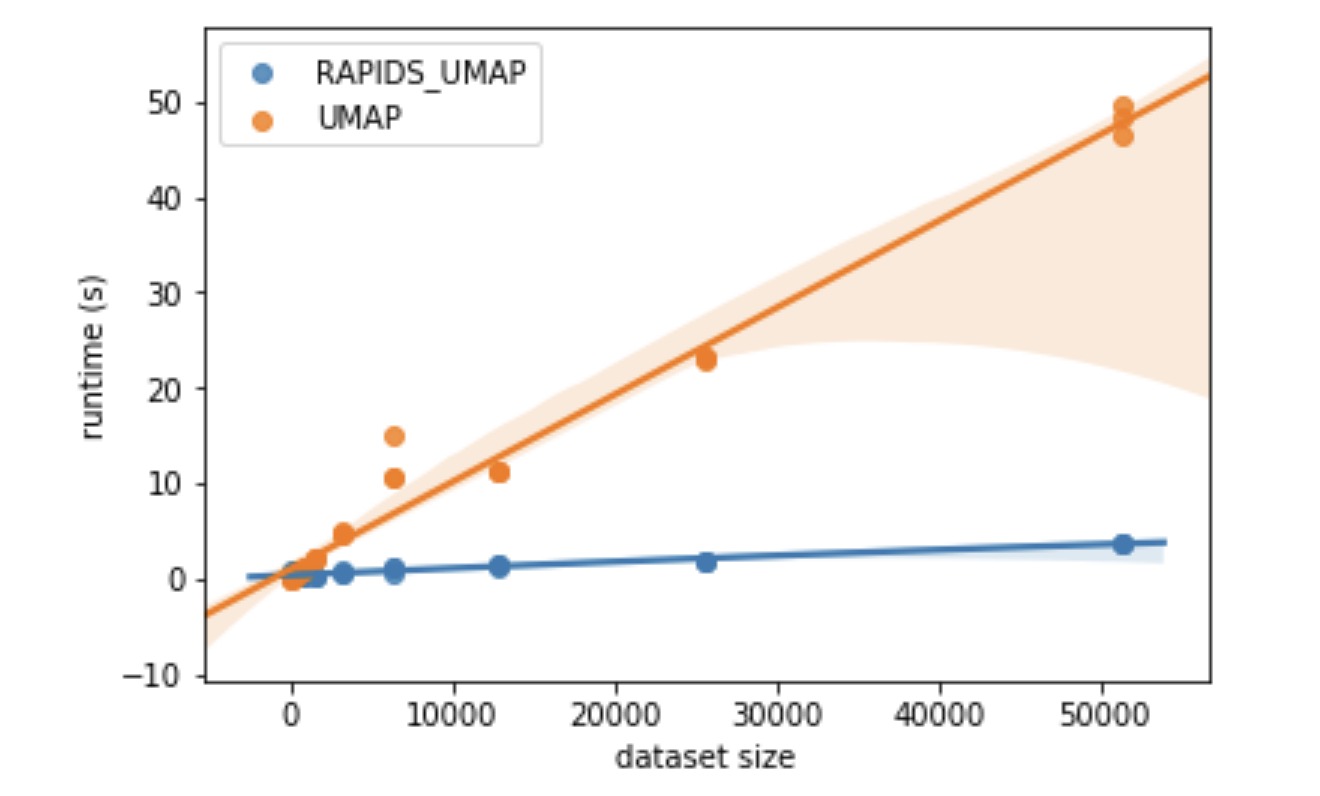
I ran a cursory MNIST benchmark based on UMAPs benchmarking suggestions, and times massively improved under RAPIDS - further investigation is definitely warranted.
This is all pretty impressive stuff, but bear in mind it might be a bit bleeding edge, depending on your viewpoint & development context. The UMAP GitHub repo hasn't reached a 1.0 version yet, but it's very promising, and definitely fulfills a need. So try it out, I'm interested in what others think!